アルキメデス

1.1. 幼少期と教育

アルキメデスは紀元前287年頃、マグナ・グラエキアの自治植民都市であるシチリア島のシラクサで生まれました。この生年は、ビザンチン時代のギリシアの歴史家ジョン・ツェツェスが主張した、アルキメデスは満75歳で没したという意見から導かれています。『砂の計算』の中でアルキメデスは、父親を無名の天文学者「ペイディアス」と告げています。プルタルコスは著書『対比列伝』にて、シラクサを統治していたヒエロン2世の縁者だったと記していますが、キケロは彼が謙虚な出自であった可能性を示唆しています。

アルキメデスは、サモスのコノンやエラトステネスがいた古代エジプトのアレクサンドリアで学問を修めた可能性があります。彼はサモスのコノンを友人と呼び、『方法』(アルキメデスの無限小)や『アルキメデスの牛の問題』には、エラトステネスに宛てた序文があります。特に『螺旋について』の序文では、ペルーシオンのドシセオスに宛てて「コノンが亡くなってから何年もが過ぎた」と記しており、これはアルキメデスが一部の著作を晩年に書いた可能性を示唆しています。彼が結婚していたか、子供がいたかといった個人的な詳細は不明です。

1.2. 功績

アルキメデスの生涯に関する標準的な記述は、彼の死後長い年月が過ぎてからギリシアやローマの歴史家によって書かれました。アルキメデスに関する最古の言及は、彼の死から約70年後に書かれたポリュビオスの『歴史』に見られます。この書はアルキメデス個人についてはほとんど触れず、彼が都市を防衛するために製作したとされる戦争機械に焦点を当てています。ポリュビオスは、第二次ポエニ戦争中にシラクサがローマからカルタゴに忠誠を切り替えた結果、マルクス・クラウディウス・マルケッルスとアッピウス・クラウディウス・プルケルが率いるローマ軍による紀元前213年から紀元前212年のシラクサ包囲戦が起こったと記しています。彼は、ローマ軍がシラクサの防御力を過小評価していたこと、そしてアルキメデスが設計した改良型投石機や、船を吊り上げて転覆させるクレーン状の機械など、いくつかの機械について言及しています。ローマ軍は最終的に都市を占領しましたが、アルキメデスの創意工夫によりかなりの損害を被りました。

紀元前75年、ローマの雄弁家マルクス・トゥッリウス・キケロがシチリアでクァエストルを務めていた頃、アルキメデスの墓について聞きました。場所は伝わっていませんでしたが、彼は探した末にシラクサのAgrigentine門の近く、低木が繁る省みられない場所に墓を見つけ出しました。キケロが墓を清掃させたところ、彫刻がはっきり分かるようになり、詩を含む碑文も見出せるようになりました。この墓には、アルキメデスが最も誇りに思っていた数学的証明、すなわち球の体積と表面積が外接する円筒のそれぞれ2/3であるという図が彫られていました。キケロはまた、マルケッルスがアルキメデスが製作した2台のプラネタリウムをローマに持ち帰ったことにも言及しています。ローマの歴史家リウィウス(紀元前59年 - 紀元17年)も、ポリュビオスのシラクサ占領とアルキメデスの役割に関する物語を語り直しています。

1.3. 死

プルタルコス(紀元45年 - 119年)は、シラクサが陥落した後のアルキメデスの死について少なくとも2つの記述を残しています。最も広く知られた記述によると、アルキメデスは都市が占領された際に数学の図形を考察していました。ローマ兵が彼にマルケッルスに会いに来るよう命じましたが、彼は問題を解き終えなければならないと言って拒否しました。これに激怒した兵士は、アルキメデスを剣で殺害しました。別の話では、アルキメデスが数学の道具を運んでいる最中に、兵士がそれを価値あるものと誤解して殺害されたとされています。マルケッルスはアルキメデスの死に激怒したと伝えられています。彼はアルキメデスを貴重な科学的資産と見なし(アルキメデスを「幾何学のブリアレウス」と呼びました)、危害を加えないよう命じていたからです。

アルキメデスの最期の言葉とされるのは「私の円をこわすな！(Noli turbare circulos meos_{ノーリー・トゥルバーレ・キルクルス・メオス}^ラテン語；μὴ μου τοὺς κύκλους τάραττε_{メー・ムー・トゥース・キュークルース・タラッテ}^{現代ギリシア語})」です。これは、彼がローマ兵に邪魔された際に研究していたとされる数学の図形を指しています。しかし、アルキメデスがこれらの言葉を実際に発したという信頼できる証拠はなく、プルタルコスの記述には登場しません。同様の引用は、ヴァレリウス・マクシムス(紀元30年頃活動)の著作『記憶すべき言行録』に見られ、「...しかし、手で砂塵を守りながら『どうか、これを邪魔しないでくれ』と言った」と記されています。

アルキメデスの墓は、彼自身が最も誇りに思っていた数学的証明を題材に選ばれ、同じ径と高さを持つ球と円筒のデザインがなされたと伝えられていました。彼が亡くなってから137年後の紀元前75年、ローマの雄弁家キケロがシチリアでクァエストルを務めていた頃、アルキメデスの墓について聞きました。場所は伝わっていませんでしたが、彼は探した末にシラクサのAgrigentine門の近く、低木が繁る省みられない場所に墓を見つけ出しました。キケロが墓を清掃させたところ、彫刻がはっきり分かるようになり、詩を含む碑文も見出せるようになりました。

2.1. 取り尽くし法と無限小

アルキメデスは、現代の積分法と同様の方法で無限小の概念を使用することができました。彼は背理法(reductio ad absurdum_{レドゥクティオー・アド・アブスルドゥム}^ラテン語)を用いることで、解が存在するある範囲を限定し、任意の精度で問題の答えを導き出すことができました。この技術は「取り尽くし法」として知られ、彼はこれを用いて図形の面積や円周率(π)の近似値を求めました。

2.2. 円周率の計算

アルキメデスは、『円周の測定』において、円周率(π)の近似値を導き出しました。彼は、一つの円に外接する正多角形と、円に内接する正多角形を想定しました。これらの正多角形は、辺の数を増やせば増やすほど円そのものに近似していきます。アルキメデスは正96角形を用いて円周率を試算し、その値が3と1/7(約3.1429)と3と10/71(約3.1408)の間にあるという結果を得ました。この近似値は、実際のπの値(約3.1416)と非常に近いものでした。彼はまた、円の面積がπに円の半径の二乗を乗じた値(πr²)に等しいことを証明しました。

『円周の測定』の中で、アルキメデスは3の平方根が265/153(約1.7320261)と1351/780(約1.7320512)の間にあると導きました。実際の3の平方根は約1.7320508であり、これは非常に正確な見積もりでした。しかし、彼はこの結果をどのようにして得たかについて、いかなる説明も提供していません。このアルキメデスの仕事の側面は、ジョン・ウォリスに「まるで意図的に自身の調査の痕跡を隠したかのようだ。あたかも彼が探求の方法の秘密を後世に惜しみ、その結果への同意を彼らから強要しようとしたかのようだ」と述べさせました。彼がこれらの値を計算するために反復的な手順を用いた可能性も指摘されています。

2.3. 幾何学

アルキメデスは、円の面積、球の表面積と体積、放物線下の面積、その他の幾何学的図形に関する重要な導出を行いました。
『球と円柱について』では、彼は自身が最も誇りに思う結果、すなわち球とそれに外接する同じ高さと直径を持つ円筒との関係を導き出しました。半径rの球の体積は4/3πr³、表面積は4πr²です。一方、同じ半径rと高さ2rを持つ円筒の体積は2πr³、表面積は6πr²(両底面を含む)となります。このことから、球の体積と表面積は常に外接する円筒のそれぞれ2/3になることを証明しました。彼の墓には、この発見を象徴する球と円筒の彫刻が施されています。

『放物線の求積法』では、アルキメデスは放物線と直線で囲まれた面積が、対応する内接三角形の面積の4/3倍に等しいことを証明しました。彼はこの問題の解を、公比が1/4の無限幾何級数として表現しました。
:$\backslash sum\_\{n=0\}^\backslash infty\; 4^\{-n\}\; =\; 1\; +\; 4^\{-1\}\; +\; 4^\{-2\}\; +\; 4^\{-3\}\; +\; \backslash cdots\; =\; \{4\backslash over\; 3\}.\; \backslash ;$
この級数の最初の項が三角形の面積であるとすると、2番目の項は、2つのより小さな割線を底辺とし、放物線の軸に平行で底辺の中点を通る線が放物線と交わる点を第3の頂点とする2つの三角形の面積の合計であり、以下同様に続きます。この証明は、合計が1/3となる級数1/4 + 1/16 + 1/64 + 1/256 + ...の変形を使用しています。

2.4. アルキメデスの性質

『球と円柱について』の中で、アルキメデスは、いかなる大きさも、それ自身を十分に何度も加えることで、任意の与えられた大きさを超えることができるという公理を提唱しました。今日、これは実数のアルキメデスの性質として知られています。

2.5. 巨大数の表現 (砂の計算)

『砂の計算』(Ψαμμίτης_{プサンミテス}^{古代ギリシア語})の中で、アルキメデスは宇宙を満たすのに必要な砂粒の数を計算しようとしました。彼は、砂粒の数が数えきれないほど多いという当時の考えに異議を唱え、次のように記しています。「ゲロン王よ、砂の数が無限であると考える者もいる。そして私が言う砂とは、シラクサやシチリアの残りの地域だけでなく、居住されているか否かにかかわらず、あらゆる地域で見つかる砂をも意味する。」

この問題を解決するために、アルキメデスは「ミリアド」(μυριάς_{ミュリアス}^{古代ギリシア語}、10,000を意味するギリシア語)を基にした数え方の体系を考案しました。彼は、ミリアドのミリアド(1億、すなわち10,000 × 10,000)の累乗を用いた数体系を提案し、宇宙を満たすのに必要な砂粒の数は8ヴィジンティリオン、すなわち8×10⁶³を超えないと結論付けました。この著作の序文では、アルキメデスの父がペイディアスという天文学者であったことが述べられています。『砂の計算』は、アルキメデスが自身の天文学に関する見解を論じた唯一現存する著作です。

2.6. 主要な数学的著作

アルキメデスの数学的著作は、彼の死後、長らくその重要性が十分に認識されていませんでしたが、後世の数学者たちに大きな影響を与えました。

• 『平面の釣合について』(Περὶ ἐπιπέδων ἱσορροπιῶν_{ペリ・エピペードーン・ヒソロピオーン}^{古代ギリシア語})
  • 2巻からなり、第1巻には7つの公理と15の提議、第2巻には10の提議が含まれています。アルキメデスはここでてこの法則を証明し、様々な幾何学的図形(三角形、平行四辺形、放物線など)の面積と重心を計算する原理を導き出しました。
• 『円周の測定』(Κύκλου μέτρησις_{キュークルー・メートレーシス}^{古代ギリシア語})
  • 3つの提議からなる短い著作で、ペルーシオンのドシセオスへの書簡形式で書かれています。第2の提議では、円周率πが223/71と22/7の間にあることを示し、後者の分数は中世から現代に至るまで円周率の近似値として広く用いられています。
• 『砂粒を数えるもの』(Ψαμμίτης_{プサンミテス}^{古代ギリシア語})
  • 宇宙を満たす砂粒の数を計算するという壮大な問題に挑戦した著作です。彼は巨大数を表現するための独自の体系を考案し、宇宙全体を埋め尽くす砂粒の数が8×10⁶³を超えないことを示しました。この著作は、アルキメデスが天文学に関する見解を述べた唯一現存するものです。
• 『平面の釣合について』(Περὶ ἐπιπέδων ἱσορροπιῶν_{ペリ・エピペードーン・ヒソロピオーン}^{古代ギリシア語})
  • 2巻からなり、第1巻には7つの公理と15の提議、第2巻には10の提議が含まれています。アルキメデスはここでてこの法則を証明し、様々な幾何学的図形(三角形、平行四辺形、放物線など)の面積と重心を計算する原理を導き出しました。
• 『放物線の求積法』(Τετραγωνισμὸς παραβολῆς_{テトラゴーニスモス・パラボレース}^{古代ギリシア語})
  • ドシセオスに宛てた24の提議からなる著作で、放物線と直線で囲まれた面積が、対応する内接三角形の面積の4/3倍に等しいことを2つの方法で証明しました。彼はこの証明に、公比が1/4の無限幾何級数を用いました。
• 『球と円柱について』(Περὶ σφαίρας καὶ κυλίνδρου_{ペリ・スファイラス・カイ・キュリンドルー}^{古代ギリシア語})
  • ドシセオスに宛てた2巻からなる著作で、アルキメデスが最も誇りに思っていた成果である、球とそれに外接する円筒との関係を導き出しました。球の体積と表面積が、それぞれ外接する円筒の2/3であることを示しました。
• 『螺旋について』(Περὶ ἑλίκων_{ペリ・ヘリコーン}^{古代ギリシア語})
  • これもドシセオスに宛てた28の提議からなる著作で、現在「アルキメデスの螺旋」と呼ばれる曲線を定義しました。これは、一定の角速度で回転しながら定速度で固定点から遠ざかる点の軌跡として記述され、現代の極座標系(r, θ)ではr = a + bθの式で表されます。これは、ギリシア数学において機械的な曲線(動く点によって描かれる曲線)が考察された初期の例です。
• 『円錐と球体について』(Περὶ κωνοειδέων καὶ σϕαιοειδέων_{ペリ・コノエイデオン・カイ・スファイロエイデオン}^{古代ギリシア語})
  • ドシセオスに宛てた32の提議からなる著作で、円錐、球、放物線の切片の面積と体積を計算する方法を示しました。
• 『浮体の原理』(Περὶ τῶν ἐπιπλεόντων σωμάτων_{ペリ・トーン・エピプレオントーン・ソーマトーン}^{古代ギリシア語})
  • 2巻からなる著作です。第1巻では流体の平衡の法則を述べ、水が重心の周りで球状に均衡することを証明しました。これは、エラトステネスのような同時代のギリシア天文学者の地球球体説を説明しようとした試みかもしれません。第2巻では、彼は放物線の切片の平衡位置を計算し、その一部は氷山のように水中に底部があり、水上に頂部がある形状を扱っており、これは船体の形状の理想化と考えられます。
  • アルキメデスの浮力の原理は、この著作で次のように述べられています。

  :どのような物体であっても全体、または一部が液体に浸かっているとき、その物体が置き換えた体積と同じだけの液体が持つ質量と同じだけの力が、方向を逆にして、物体を押し上げる。

  • 『ストマッキオン』(Στομάχιον_{ストマキオン}^{古代ギリシア語}、Ὀστομάχιον_{オストマキオン}^{古代ギリシア語})
    • 「アルキメデスの小筥」とも呼ばれる、タングラムに似た切断パズルです。この著作は、アルキメデス・パリンプセストの中でより完全な形で発見されました。アルキメデスは、正方形を形成するために組み立てられる14個のピースの面積を計算しました。スタンフォード大学のリヴィエル・ネッツは2003年に、アルキメデスがこれらのピースを正方形に組み立てる方法の数を特定しようとしていたと主張し、それが17,152通りあると計算しました。回転や反転によって等価な解を除外すると、配置の数は536通りとなります。このパズルは、組み合わせ数学における初期の問題の一例です。
    • パズルの名前の由来は不明ですが、ギリシア語で「喉」や「食道」を意味するstomachos(στόμαχος_{ストマコス}^{古代ギリシア語})に由来するという説があります。アウソニウスは、このパズルをOstomachionと呼びました。これは、骨(ὀστέον_{オステオン}^{古代ギリシア語}、osteon)と戦い(μάχη_マケー^{古代ギリシア語}、machē)の語根から形成されたギリシア語の複合語です。
  • 『アルキメデスの牛の問題』
    • 1773年にゴットホルト・エフライム・レッシングがドイツのヴォルフェンビュッテルにあるヘルツォーク・アウグスト図書館で発見した、44行の詩からなるギリシア語の写本に記されています。これはエラトステネスとアレクサンドリアの数学者たちに宛てられたもので、アルキメデスは彼らに、いくつかの連立ディオファントス方程式を解くことで、太陽の牛の群れの数を数えるよう挑戦しました。この問題には、一部の解が平方数であるというより難しいバージョンがあります。A.アムトールが1880年にこのバージョンの問題を初めて解き、その答えは約7.760271×10²⁰⁶⁵⁴⁴という非常に大きな数となりました。
  • 『方法』(Περὶ μηχανικῶν θεωρημάτων πρὸς Ἐρατοσθένη ἔφοδος_{ペリ・メーカニコーン・テオーレーマトーン・プロス・エラトステネー・エフォドス}^{古代ギリシア語})
    • この論文は、1906年にアルキメデス・パリンプセストが発見されるまで失われたと考えられていました。この著作でアルキメデスは無限小の概念を用い、図形を無限に小さな部分に分解することで、その面積や体積をどのように決定できるかを示しています。彼はこの方法が形式的な厳密さに欠けていると考えたため、結果を導き出すために取り尽くし法も用いた可能性があります。『牛の問題』と同様に、『方法』もアレクサンドリアのエラトステネスに宛てた書簡の形式で書かれています。

2.7. 散逸した著作

アルキメデスの多くの著作は現存しておらず、他の古代の著述家による言及を通じてのみ知られています。これらには、アレクサンドリアのパップスが言及した『球体製作について』や多面体に関する別の著作、アレクサンドリアのテオンが引用した光学に関する失われた著作『カトプトリカ』(反射光学)などが含まれます。また、ゼウクシッポスに宛てられ、『砂の計算』で用いられた数体系を説明した『原理』、てこや重心に関する著作、そして暦に関する著作も失われたとされています。

アルキメデスの『補助定理集』(『リベル・アッスンプトルム』)は、円の性質に関する15の提議を扱った論文ですが、現存する最古の写本はアラビア語で書かれています。T.L.ヒースやマーシャル・クラーゲットといった学者は、現在の形ではアルキメデス自身が書いたとは考えにくいと主張しており、これはアルキメデスを引用していることから、別の著者によって修正された可能性を示唆しています。『補助定理集』は、現在失われたアルキメデスの初期の著作に基づいている可能性があります。

また、三角形の3辺の長さからその面積を計算するヘロンの公式もアルキメデスに知られていたと主張されることがありますが、この公式の最初の信頼できる記述は、紀元1世紀のアレクサンドリアのヘロンの著作に見られます。アルキメデスの著作とされるその他の疑わしい帰属には、紀元4世紀または5世紀のラテン語詩『カルメン・デ・ポンデリブス・エト・メンスリス』(王冠の問題を解決するための静水圧天秤の使用を記述)や、12世紀のテキスト『マッパエ・クラヴィキュラ』(比重を計算して金属を分析する方法に関する指示を含む)があります。

2.8. アルキメデス・パリンプセスト

アルキメデスの著作を含む最も重要な文書は「アルキメデス・パリンプセスト」です。1906年、デンマークの教授ヨハン・ルーズヴィー・ハイベアは、コンスタンティノープルを訪れ、13世紀に書かれた174ページの山羊皮紙の祈りの書を調査しました。彼はそれがパリンプセスト、つまり消された古い著作の上に新しいテキストが書かれた文書であることを確認しました。パリンプセストは、高価な羊皮紙を再利用するために、既存の著作からインクを削り取って再利用する中世の一般的な慣行でした。パリンプセスト内の古い著作は、学者たちによって、それまで失われたと考えられていたアルキメデスの論文の10世紀の写本であると特定されました。この羊皮紙は、コンスタンティノープルの修道院図書館に何百年も保管された後、1920年代に個人収集家に売却されました。1998年10月29日、ニューヨークのクリスティーズで匿名購入者に合計220.00 万 USDで落札されました。

このパリンプセストには、ギリシア語の原典で唯一現存する『浮体の原理』を含む7つの論文が収録されています。また、スーダ辞典に言及され、永遠に失われたと考えられていた『方法』の唯一の既知の情報源でもあります。『ストマッキオン』もこのパリンプセストで発見され、以前のテキストよりも完全なパズルの分析が含まれていました。パリンプセストは現在、メリーランド州ボルチモアのウォルターズ美術館に保管されており、上書きされたテキストを読み取るために紫外線やX線などの様々な現代的な検査が施されています。

アルキメデス・パリンプセストに含まれる論文は以下の通りです。

• 『平面の釣合について』
• 『螺旋について』
• 『円周の測定』
• 『球と円柱について』
• 『浮体の原理』
• 『方法』
• 『ストマッキオン』
• 紀元前4世紀の政治家ヒュペレイデスの演説
• アリストテレスの『範疇論』に関する注釈書
• その他の著作

3.1. 数学・物理学への影響

科学史家や数学史家は、アルキメデスが古代最高の数学者であったという点でほぼ普遍的に同意しています。例えば、エリック・テンプル・ベルは次のように記しています。
:歴史上「最も偉大な」数学者3人のリストには、必ずアルキメデスの名前が含まれるだろう。彼と並び称される他の2人はアイザック・ニュートンとカール・フリードリヒ・ガウスである。しかし、これらの巨人が生きたそれぞれの時代の数学と物理科学の相対的な豊かさ(あるいは貧困さ)を考慮し、彼らの業績をその時代の背景に対して評価するならば、アルキメデスを第一位に置く者もいるだろう。
同様に、アルフレッド・ノース・ホワイトヘッドとジョージ・F・シモンズはアルキメデスについて次のように述べています。
:...1500年には、ヨーロッパは紀元前212年に亡くなったアルキメデスよりも知識が少なかった...
:もし、他のすべての人々が、時間の始まりから17世紀の西ヨーロッパに至るまで、あらゆる大陸、あらゆる文明において数学と物理学で達成したことを考慮するならば、アルキメデスの業績はそれらすべてを凌駕する。彼はそれ自体で一つの偉大な文明であった。
スタンフォード大学のギリシア数学・天文学教授であり、アルキメデスの専門家であるリヴィエル・ネッツは次のように述べています。
:そして、アルキメデスが誰よりも微積分学の形成を導き、物理世界への数学の応用を開拓したことから、西洋科学はアルキメデスへの一連の脚注に過ぎないことが判明する。したがって、アルキメデスは史上最も重要な科学者である。
レオナルド・ダ・ヴィンチは繰り返しアルキメデスへの賞賛を表明し、自身の発明であるアルシトネールをアルキメデスに帰属させました。ガリレオ・ガリレイは彼を「超人的」で「私の師」と呼び、クリスティアーン・ホイヘンスは「アルキメデスに匹敵する者はいないと思う」と述べ、初期の著作で意識的に彼を模倣しました。ゴットフリート・ヴィルヘルム・ライプニッツは「アルキメデスとペルガのアポロニウスを理解する者は、後世の最も優れた人々の業績をそれほど賞賛しないだろう」と述べました。ガウスの英雄はアルキメデスとニュートンであり、ガウスの下でゲッティンゲン大学で学んだモーリッツ・カントールは、彼がかつて「画期的な数学者はアルキメデス、ニュートン、ゴットホルト・アイゼンシュタインの3人だけだった」と語ったと報告しています。

発明家ニコラ・テスラは彼を称賛し、次のように述べています。
:アルキメデスは私の理想でした。私は芸術家の作品を賞賛しましたが、私の考えでは、それらは影と見せかけに過ぎませんでした。発明家は、触れることができ、生き、機能する創造物を世界に与えるのだと私は思いました。

3.2. 記念と表彰

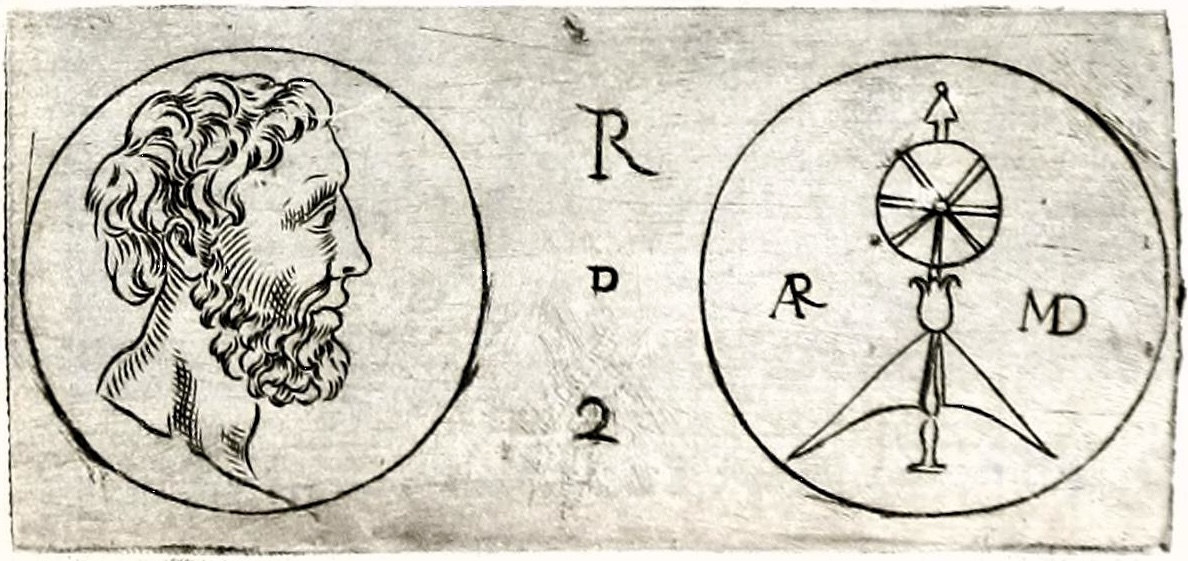
イタリアの貨幣学者で考古学者のフィリッポ・パルータ(1552年 - 1629年)とレオナルド・アゴスティーニ(1593年 - 1676年)は、シチリアで発見された青銅貨について報告しました。その表側にはアルキメデスの肖像が、裏側には円筒と球体がラテン語のモノグラムARMDと共に描かれていました。この貨幣は現在失われており、その正確な年代は不明ですが、イヴォ・シュナイダーは裏側を「台座に乗った球体 - おそらくアルキメデスが製作したプラネタリウムの一つを大まかに描いたもの」と記述し、マルケッルスが「古代の報告によれば、アルキメデスの球体を2つローマに持ち帰った」ことから、ローマで鋳造された可能性を示唆しました。

月の北緯29.7度、西経4.0度には、彼を称えてアルキメデス・クレーターが命名されており、また月の山脈であるモンテス・アルキメデス(北緯25.3度、西経4.6度)も彼の名にちなんでいます。

数学における傑出した業績を称えるフィールズ・メダルには、アルキメデスの肖像と、球と円筒に関する彼の証明を示す彫刻が施されています。アルキメデスの頭部の周りの碑文は、紀元1世紀の詩人マルクス・マニリウスに帰属される引用句であり、ラテン語で「Transire suum pectus mundoque potiri_{トランシーレ・スウム・ペクトゥス・ムンドークエ・ポティーリー}^ラテン語」(己を超え、世界を掌握せよ)と記されています。

アルキメデスは、東ドイツ(1973年)、ギリシア(1983年)、イタリア(1983年)、ニカラグア(1971年)、サンマリノ(1982年)、スペイン(1963年)が発行した切手にも登場しています。

アルキメデスに帰属される感嘆詞「ユリーカ！」は、カリフォルニア州の州の標語となっています。この場合、この言葉は1848年にサッターズミル近くで金が発見され、カリフォルニア・ゴールドラッシュが始まったことを指しています。